계속 나오는 VAE! 공부해보자

해당 포스트는 이활석님의 “오토인코더의 모든 것”강의를 정리한 포스트입니다.

contents

1. revisit DNN
2. manifold learning
3. AutoEncoder
4. Variational AutoEncoder
5. Application

AutoEncoder

AutoEncoder는 인공신경망 네트워크의 일종으로, 차원축소를 목적으로 데이터의 representation을 학습하기 위한 네트워크이다. 최근에는 AE(AutoEncoder)가 generative model분야에서 자주 사용된다고 한다.

오토인코더의 구조

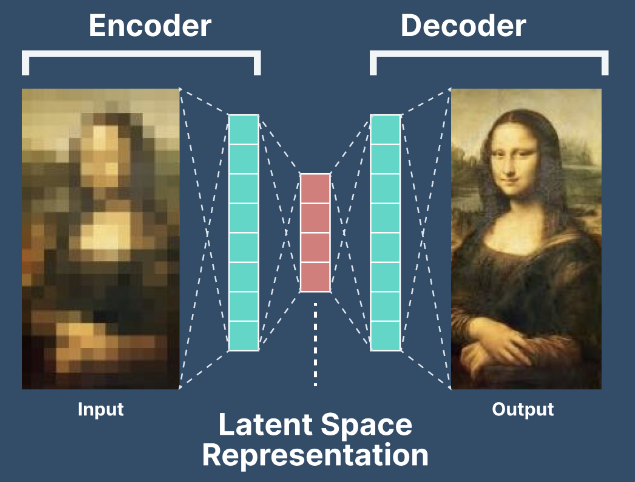
오토인코더는 다음과 같이 인코더와 디코더가 붙어 있는 구조를 갖고 있다. 오토인코더는 비지도학습의 일종이며 loss는 negative Maximum Likelihood로 해석된다. 학습완료 후 인코더는 차원축소 모델로 기능하고 디코더는 생성모델로 기능한다.

AutoEncoder에 대한 키워드는 4가지로 볼 수가 있다.

1. Unsupervised learing : 비지도학습, 학습시 라벨링이 필요가 없다!
2. manifold learning: 고차원의 공간 전체에 중요한 정보가 퍼져 있는게 아니다. 정보가 몰려 있는 manifold 공간을 찾아 차원을 축소시키자.
3. generative model learning: 모델 내 생성파트가 존재한다.
4. Maximum Likelihood density estimation: 우도를 최대화하는 density를 예측한다.

autoencoder를 본격적으로 들어가기 전 먼저 필요한 DNN에 대한 이해를 해보도록 하자.
(굳이 DNN에 대해서 다루는 이유는 loss를 MLE관점에서 해석한다는 의미를 이해하기 위해서이다.)

revisit DNN

고전적 머신러닝의 방법론을 순서대로 생각해보자.

1. 먼저 데이터셋을 모은다. (X, y)
2. X를 가지고 y를 설명할 좋은 방법은 없을까? 가장 좋은 설명을 하는 model $f_{\theta}()$를 정의한다. 이때 모델은 theta의 함수이다.
3. Loss는 target과 예측값의 차이다. 원하는 Loss 함수를 정의한다. 이때 Loss는 target과 예측값(model에 X를 대입한 값)에 대한 함수이다.
4. learning 과정은 Loss를 최소화하는 $\theta$를 찾는 과정이다. 이때 closed form으로 argmin Loss가 주어지면 좋지만 그렇지 않을 경우 gradient descent 방법과 같은 iterative한 방법을 적용한다.
5. 4번 과정을 통해 얻은 최적의 $\theta$를 f에 대입하여 최종 모델을 얻는다. model에 새로운 x데이터를 대입한 $f_{\theta}$가 $y_{new}$와 가까운지를 본다. (predict)

정리하자면 데이터를 모은 뒤, 데이터를 잘 설명하는 model을 정의하고 loss ftn을 정의한다. loss ftn은 X, y, $\theta$의 함수이지만 X, y는 realized value이므로 결국 loss ftn은 $\theta$의 함수이다. 이 loss를 최소화하는 $\theta$를 찾는게 목적이지만 closed form으로 구할 수 없을 경우 GD같은 방법을 이용해 구한다.

deep learning에서 자주 사용되는 loss ftn은 MSE, cross entropy 두가지이다. 다른 loss 함수도 많은데 왜 이 두가지가 자주 사용되는 걸까?

딥러닝처럼 복잡한 모델에 대해서 학습을 할 때는 gradient descent를 구하기 위해서 필요한 gradient가 단순하게 구해지지 않는다. layer를 통과할 때마다 구해지는 gradient의 곱을 이용하는 back propagation 알고리즘을 통해 weight update를 하게 되는데 back prop을 하기 위해서는 loss ftn에 두가지 제약이 따른다.

1. training DB의 전체 데이터에 대한 loss가 sample 데이터에 대한 loss의 합이다.
2. sample별 loss ftn의 입력인자는 label과 neural network의 출력값 두가지여야 한다.

이러한 제약을 만족시키는 MSE, Cross Entropy와 같은 loss ftn이 backprop이 필요한 DNN에 자주 사용되는 것이다.

loss를 해석하는 두가지 관점

그렇다면 loss를 해석하는 두가지 관점에 대해서 생각해보자.

1 back prop 관점에서 해석

“loss를 줄이는 방향으로 업데이트”

$L(y, f_{\theta}(x) )$를 최소화하기 위해 backprop Cross Entropy와 MSE 중에서 Cross Entropy가 더 backprop이 더 잘된다. (수식상 절묘하게 vanishing gradient에 강인)

2 Maximum Likelihood Estimation 관점에서 해석

“네트워크 출력값을 미리 정해둔 분포의 파라미터로 해석”

$f_{\theta}(.)$이 모델이고, $p(y|f_{\theta}(x))$이 정해진 확률분포에서 출력(y)이 나올 확률일 때, 예측값 $f_{\theta}(x)$은 정해진 확률분포의 모수로 해석할 수 있다.

예를 들어 위의 그림과 같이 정해진 확률분포가 정규분포라고 할 때, $f_{\theta1}(x) = 3$에서 $\theta$가 업데이트되어 $f_{\theta2}(x) = 5$가 될 경우, 정규분포의 평균이 3에서 5로 업데이트된 것으로 볼 수 있다. 이 때 y=6이라면 평균이 3인 정규분포보다는 5인 정규분포에서 뽑힌 값일 확률이 더 높으므로 올바른 방향으로 업데이트 된 것으로 생각할 수 있다. 이를 수식으로 나타내면, $\theta^* = argmin[-logp(y|f_{\theta})(x)]$로 볼수 있다. 이 수식의 의미는 negative log likelihood를 최소화하는 $\theta$는 MLE로 볼 수 있다.

\[y_{new} \sim p(y|f_{\theta^*}(x_{new}))\]

이때 모수는 $f_{\theta^*}(x_{new})$

위 수식과 같이 해당 분포에서 y가 확정적(deterministic)으로 결정되는 것이 아니라 $y_{new}$를 샘플링할 수 있다.

미리 정해진 분포로는 흔히 가우시안 분포 또는 베르누이 분포를 사용한다. 이를 수식으로 풀어보자.

1 가우시안 분포: Mean Square Error

$f_{\theta}(x_i) = \mu_{i}, \sigma_{i} = 1$
$p(y_{i}|\mu_{i},\sigma_{i}) = {1 \over \sqrt{2\pi} \sigma_{i}}exp{-(y_{i}-\mu_{i})^2 \over {2\sigma_{i}^2}}$
$logp(y_{i}|\mu_{i},\sigma_{i}) = log{1 \over \sqrt{2\pi} \sigma_{i}}-{(y_{i}-\mu_{i})^2 \over 2\sigma_{i}^2}$
$-logp(y_{i}|\mu_{i}) = -log{1 \over \sqrt{2\pi}}+{(y_{i}-\mu_{i})^2 \over 2}$
$-logp(y_{i}|\mu_{i}) \propto {(y_{i}-\mu_{i})^2 \over 2 } = {(y_{i}-f_{\theta}(x_{i}))^2 \over 2}$

y의 분포를 정규분포로 가정하고 negative log likelihhood를 최소화하는 과정은 결국 backprop관점에서 MSE를 최소화하는 과정과 같다.

2 베르누이 분포: cross-entropy

$p(y_{i} \mid p_{i}) = p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}}$
$log(p(y_{i} \mid p_{i})) = y_{i}log(p_{i})+(1-y_{i})log(1-p_{i})$
$-log(p(y_{i} \mid p_{i})) = -y_{i}log(p_{i})-(1-y_{i})log(1-p_{i})$

y의 분포를 베르누이로 가정하고 negative log likelihhood를 최소화하는 것은 결국 backprop관점에서 cross entropy를 최소화하는 것과 같다.

이러한 이유로 연속확률분포에 대해서는 MSE를 loss ftn으로 사용하고 이산확률분포에서는 cross entropy를 loss ftn으로 사용하는 것이 자연스럽다.

manifold learning

고차원데이터는 training db의 차원 그 자체인데, 이를 데이터 공간에 쫙 뿌렸을 때 이러한 데이터를 잘 아우르는 subspace를 manifold라고 한다. manifold를 찾고 그 위로 데이터를 정사영한다면 데이터의 정보를 많이 잃지 않고도 차원을 줄일 수 있다. 이때 차원을 줄이는 과정을 manifold learing이라고도 한다. 차원축소를 통해 아래와 같은 기능을 얻을 수 있다.

1. 데이터 압축
2. 데이터 시각화
3. 차원의 저주 극복
4. 중요한 features 찾기

manifold hypothesis

• 고차원의 데이터는 밀도가 낮지만 이들의 집합을 포함하는 저차원의 manifold가 있다.
• 이 저차원의 manifold를 벗어나는 순간 밀도가 급격히 낮아진다.

만약 manifold 가정이 사실이 아니라면 유니폼 샘플링했을 때 의미있는 데이터가 도출되어야 한다. 그러나 현실에서 유니폼 샘플링을 해보면 거의 대부분 노이즈가 도출된다. 매니폴드를 잘 찾으면 서로 다른데 비슷한 데이터간의 관계를 알아낼 수 있다. 매니폴드 학습 결과를 평가하기 위해 매니폴드 좌표들이 조금씩 변할 때 원데이터도 유의미하게 조금씩 변한다.

resonable distance metric

원래 데이터 공간에서의 유클리디안 거리가 가까운 대상과 메니폴드상에서의 유클리디안 거리가 가까운 대상이 다르다. 메니폴드 상에서 유클리디안이 가깝다는 뜻은 dominant한 feature들끼리 가깝다는 뜻으로, 의미상 가까운 대상일 가능성이 높다. 반대로 원래 데이터 공간에서 가까워도 의미적으로 가깝지 않은 대상일 가능성이 높다.

위 그림에서 가장 왼쪽 그림과 가장 오른쪽 그림을 나타내는 임베딩 벡터에 대해 원데이터 공간 상의 중간지점이 의미상으로 중간에 해당하는 그림이 아니라 손이 여러개인 이상한 그림으로 나타나는 것을 확인 할 수 있다.

그러나 위 그림처럼 원데이터 공간상의 중간지점이 아니라 매니폴드 공간 상의 중간지점에 대한 그림은 우리가 의도한 대로 의미상 중간지점의 그림이 나오는 것을 확인할 수 있다.

Autoencoder

2000년대 초반에 자주 쓰인 네트워크이다.입력과 출력이 같으며, 인코더 파트에서는 차원이 줄어들고, 디코더 파트에서는 차원이 늘어난다.

가운데 줄어든 latent variable이 input의 압축된 정보를 담고 있다.

따라서 오토인코더는 차원축소의 기법중 하나라고도 볼 수 있다.

이때 latent variable은 code, feature, hidden representation이라고도 부른다.

인코더의 네트워크를 h라고 하고 디코더의 네트워크를 g라고 할 때

오토인코더의 Loss는 reconstruction error로, L(x, g(h(x)))이다. 비교사학습문제에서 input, output을 동일하게 줌으로써 교사학습문제로 바꾸어 푼다는 점에서 각광을 받았다.

(자기 자신을 정답으로 가진다는 의미에서 self supervised learning이라고도 한다.)

인코더와 디코더를 떼서 각각 쓴다고 할 때, 인코더는 적어도 training data에 대한 압축을 잘 한다는 최소한의 성능을 보장할 수 있고, 디코더는 적어도 training data에 대한 생성은 잘 해낼 수 있다는 최소한의 성능을 보장할 수 있다. (GAN은 이러한 최소한의 성능보장은 불가능하다.)

위 그림처럼 input이 인코더로 들어가면 latent vector로 압축되고 이것이 decoder로 들어가 복원한다. 이때 input과 네트워크 출력값을 비교한 loss를 training DB 전체에 대해 더해서 최종 loss를 구한다.

만약 여기에서 activation ftn없이 사용하면 Linear Autoencoder라고 부른다. 그런데 신기하게도 Linear autoencoder를 사용하고 loss를 MSE로 사용하면 PCA와 똑같은 manifold를 배운다. 정확히 똑같은 basis를 갖진 않지만 똑같은 subspace를 구성한다.

stacking Autoencdoer

2000년대 초반에 자주 쓰인 오토인코더는 차원축소와 더불어 모델의 초기화에 자주 쓰이는 방법론이었다.(지금은 안쓴다.) DNN에 대해서 layer by layer로 pretraining을 시켰다. 현재의 레이어에 대해 다음레이어로 간다음 다시 현재레이어로 돌아오도록 하는 weight로 가중치를 초기화한 것이다. 이때 인코더부분에 해당하는 W와 디코더부분에 해당하는 W’는 transpose관계에 있는 똑같은 weight로 학습tied weights시킨다.

Denosing Autoencoder

x에 noise가 추가된 버전이 인코더와 디코더를 통과하면 x로 복원되도록 학습한 모델이 DAE이다.

noise를 추가시킨 x를 네트워크에 넣으면 noise가 없어진 버전인 x가 도출된다고 하여 denoising(노이즈를 없애다) 오토인코더라는 이름이 붙었다. latent vector를 잘 찾았다는 것은 manifold 공간을 잘 찾았다는 의미라고 해석할 수 있다. manifold 공간을 잘 찾았다는 것은 다차원 공간 속에서 유의미한 정보에 대한 공간을 찾았다고 생각할 수 있다. 이미지 데이터를 DAE에 집어 넣었다고 생각해보자. 이때 이미지의 픽셀은 약간 변화했지만 사람의 눈으로는 크게 차이가 없도록 노이즈를 추가했다고 하자. 이런 상황에서 DAE의 인코더 파트가 manifold를 잘 학습했다면 원본이미지에 대한 manifold 공간상의 점과 노이즈가 추가된 이미지에 대한 manifold 공간상의 점이 크게 다르지 않아야 한다. 따라서 x든 x에 노이즈를 추가한 것이든 latent vector이 동일하므로 디코더를 통과해 복원되었을 때도 동일할 것이라는 논리로 만든 것이 DAE다. 즉 의미상으로는 동일하나 원본 데이터 상으로는 약간 다르게 만드는 noise를 추가해줌으로써 manifold 공간을 좀 더 robust하게 잘 배우도록 만드는 것이다.

위 그림의 수식에서 $q(\tilde{x} \mid x)$는 noise를 만들어내는 분포를 표현한 것이다. noise를 더하는 방법으로는 dropout noise, gaussian noise, salt-and-pepper noise등이 있다.

위 페이지는 샘플링을 이용하여 기존의 AE를 쌓은 SAE와 DAE를 쌓은 SDAE를 비교한 그림이다.

input을 각 네트워크에 집어넣고 각 네트워크의 출력값을 베르누이분포의 모수로 해석하여 해당 베르누이분포에서 샘플링한 데이터를 비교해보았을 때 AE보다 DAE가 더 깔끔한 이미지를 만들어낸다.

CAE

contractive autoencoder는 DAE와 철학은 같지만 noise를 더한 파트를 regularizaition term으로 빼서 설명한 모델이다.

reconstruction error 파트에는 error term이 더해지지 않은 버전의 x가 네트워크를 통과한 형태의 loss이고, noise를 더한 버전과 원본 버전이 각각 인코더 파트만을 통과했을 때의 차이를 정규화 term으로 더해준 것을 loss로 사용한다.

이때 stochasitc regularization term이 계산하기 어려우므로, 위와 같이 테일러 근사를 활용한다.

VAE

대망의 VAE에 대해서 설명해 보겠다.

Variational AutoEncoder와 앞서 설명한 AutoEncoder의 비교해 보면 코드상의 차이가 없다.

그러나 VAE와 AE를 논문에서 따라가다보면 서로 완전히 다른 것처럼 보인다.

그 이유가 무엇일까?

AE는 인코더 부분에서의 manifold learning을 교사학습방법으로 만들어내기 위해 디코더가 붙은 모델이다.

즉 AE는 디코더에서의 생성에 관심이 있는 모델이라기 보다는 인코더에서 데이터를 잘 압축하는 성능에 관심이 있는 모델이다.

그러나 VAE는 정반대이다. 데이터를 만들어내기 위한 목적의 generative model로, 디코더에서 데이터를 생성하기 위해 인코더가 붙은 모델이다.

그러다 보니 구조적으로 VAE의 형태가 AE와 유사하게 된 것이다.

z가 어떤 확률분포 p(z)를 따른다고 할 때 $g_{\theta}(\cdot)$라는 디코더의 네트워크를 통과하고 나면 만들어지는 $g_{\theta}(z)$가 x와 유사하다면 $g_{\theta}(\cdot)$는 x를 잘 만들어내는 분포라고 볼 수 있다.

이때 $g_{\theta}(z)$는 우리가 정한 어떤 분포의 모수로 보고, 이에 대한 MLE인 $P(x \mid g_{\theta}(z))$를 최대화하고자 한다.

즉, $P(x \mid g_{\theta}(z)) = P_{\theta}(x \mid z)$라는 확률을 최대화하기를 원하는 것이다.

이때 z는 prior분포에서 sampling을 한 값이다. sampling을 하기 위해서는 P(z)가 다루기 쉬운 분포여야 하므로 보통 정규분포 또는 이항분포를 사용한다.

그런데 manifold 상에서의 값을 취해서 하는게 아니라 랜덤한 값에서 샘플링한다면 뭔가 안맞지 않은가?

그러나 연구에 따르면 앞의 한 두개의 layers에서 manifold 공간을 학습하기 때문에 prior dist이 간단해도 괜찮다고 한다…!

그런데 prior인 p(z)를 알고, $P(x \mid g_{\theta}(z))$도 임의로 정한 분포이니까, x,z에 대입하면 $\theta$에 대한 함수로 나오므로 여러개 뽑아서 montecarlo방식으로 합치는 방식으로 직접적으로 MLE를 해도 되지 않는가라는 의문이 들 수 있다.

그러나 이 방식에는 문제가 있다.

위 그림에서 (a)에서 한 부분을 잘라낸 것이 (b), 오른쪽으로 살짝 이동한 것이 (c)이다.

의미적으로 (a)와 (c)가 (a)와 (b)보다 더 가깝지만 $p(x \mid g(z))$ 상으로는 (b)가 더 가깝다.

$p(X \mid g(z))$상으로는 더 가까운 그림이 확률에 기여하는바가 더 크기 때문에 이러한 방식을 채택할 경우

의미적으로 거리가 먼 그림의 기여도가 더 커 올바른 확률값을 구하기가 어려울 수 있다.

임의로 정한 정규분포 등의 prior에서 z를 sampling을 하면 앞과 같은 문제가 생기므로 이상적인 sampling 함수를 정하는 방식을 도입한다.
즉 x가 evidence로 주어질 때 적어도 x는 잘 만들어내는 z를 sampling하는 분포를 찾기 위해 $p(z \mid x)$를 찾는다.
그런데 이 분포를 모르므로 $p(z \mid x)$를 variational inference방법으로 추정한다.
VI방법이란 우리가 모르지만 추정하고자 하는 $p(z \mid x)$(true posterior)이 있을 때, 다루기 쉬운 approximation class q(정규분포 등)를 정하고 이 분포의 정규분포를 결정짓는 파라미터인 $\phi$를 잘 바꿔가면서 최대한 true posterior에 가깝게 만들어 만든 $q_{\phi}(z \mid x)$를 만드는 방법이다.

이렇게 만들어진 $q_{\phi}(z \mid x)$로 z를 샘플링을 하여 generator에 넣으면 x가 잘 생성될 것이라고 기대할 수 있다.

지금까지의 상황을 정리해보면,

$p(x) = \sum_{i}p(x \mid g_{\theta}(z_{i}))p(z_{i})$로 계산시 prior인 $p(z_{i})$가 의도에 맞는 확률을 생성하지 못하므로,

$p(z \mid x)$를 도입하여 이에 대한 근사값인 $q_{\phi}(z \mid x)$를 사용한다.

이제, p(x)와 $p(z \mid x)$, $q_{\phi}(z \mid x)$의 관계를 식으로 알아보자.

유도방식 1

$p(x) = \int p(x|z)p(z)\, dz$
$log(p(x)) = log(\int p(x|z)p(z)dz) \geq (\int log(p(x|z))p(z)dz)$
$\because$ Jensen’s Identity, log 함수는 concave 함수이므로, $f(E(x))>E(f(x))$
$log(p(x)) = log(\int \frac{p(x|z)p(z)}{q_{\phi}(z|x)}q_{\phi}(z|x)\ dz) \geq \int log(\frac{p(x|z)p(z)}{q_{\phi}(z|x)})q_{\phi}(z|x)\, dz$
$\because$ Jensen’s Identity, log 함수는 concave 함수이므로, $f(E(x))>E(f(x))$
$log(p(x))\geq \int log(p(x|z))q_{\phi}(z|x)dz-\int log(\frac{q_{\phi}(z|x)}{p)(z)})q_{\phi}(z|x)dz$
$= E_{q_{\phi}(z|x)}(log(p(x|z)))-KL(q_{\phi}(z|x)|p(z))=ELBO(\phi)$

ELBO = Evidence Lower BOund

유도방식 2 : 더 흔히 사용하고 더 직관적

$log(p(x)) = \int log(p(x))q_{\phi}(z \mid x)dz \leftarrow \int q_{\phi}(z \mid x)dz=1$
$= \int log(\frac {p(x,z)}{p(z \mid x)})q_{\phi}(z \mid x)dz \leftarrow p(x) = \frac {p(x,z)}{p(z \mid x)}$
$= \int log(\frac{p(x,z)}{q_{phi}(z \mid x)}\cdot\frac{q_{phi}(z \mid x)}{p(z \mid x)})q_{\phi}(z \mid x)dz$
$= \int log(\frac{p(x,z)}{q_{\phi}(z \mid x)})q_{\phi}(z \mid x)dz + \int log(\frac {q_{\phi}(z \mid x)}{p(z \mid x)})q_{\phi}(z \mid x)dz$
$= ELBO(\phi)+KL(q_{\phi}(z \mid x)\parallel p(z \mid x))$

KL은 두 확률분포간의 거리이므로 0이상이다.

따라서 $log(p(x))$에서 0이상인 KL인 값을 뺀 것이 ELBO이므로 $ELBO(\phi)$는 $log(p(x))$보다 작거나 같다.

이상적인 sampling함수 $p(z \mid x)$와 이에 대한 근사함수인 $q_{\phi}(z|x)$이 가까울수록, 즉 분포를 잘 근사했을수록 KL이 작아진다.
KL이 작아지면 $log(p(x))$에서 0이상인 KL인 값을 뺀 것이 ELBO이므로 ELBO는 커진다.

즉 KL minimize = ELBO maximize

$argmin_{\phi}(KL(q_{\phi}(z \mid x)\parallel p(z \mid x)))= argmax_{\phi}ELBO(\phi)$

그러므로, KL을 최소화하는 문제를 ELBO를 최대화하는 문제로 바꾸어 풀 수 있다.

$ELBO(\phi) = \int log(\frac{p(x,z)}{q_{\phi}(z \mid x)})q_{\phi}(z \mid x)dz$
$= \int log(\frac {p(x \mid z)p(z)}{q_{\phi}(z \mid x)})q_{\phi}(z \mid x)dz$
$= \int log(p(x \mid z))q_{\phi}(z \mid x)dz - \int log(\frac {q_{\phi}(z \mid x)}{p(z)})q_{\phi}(z \mid x)dz$
$= E_{q_{\phi(z \mid x)}}[log(p(x \mid z))]-KL(q_{\phi}(z \mid x)\parallel p(z))$

• 주의: $logp(x)$내의 KL과는 KL term이 다르다.

정리하면 네트워크의 입력이 되는 z를 잘 뽑아주는 샘플링 함수는 $ELBO(\phi)$를 최대화하는 $\phi$를 구하여 얻을 수 있다.

네트워크를 최적화하기 위해서는 한가지 최적화를 더 해야하는데, 샘플링해서 넣은 z를 통해 generator g가 학습을 잘 해서 x를 뱉어낼 MLE를 최대화하도록 하는 $\theta$를 구하는 것이다.

즉 $E_{q_{\phi(z \mid x)}}[log(p(x \mid g_{\theta}(z)))]$가 커지기를 바란다.

그런데 $ELBO(\phi)$ 안의 $E_{q_{\phi(z \mid x)}}[log(p(x \mid z))]$가 이와 구조가 동일하다.

따라서 네트워크를 학습시키기 위한 최종적인 loss 함수는

$argmin_{\theta, \phi}\sum -E_{q_{\phi}(z \mid x_{i})}[log(p(x{i} \mid g_{\theta}(z)))]+KL(q_{\phi}(z \mid x_{i} \parallel p(z))$이다.

지금까지의 논리를 정리해보자면,

$g_{\theta}$를 통과했을 때 x를 잘 만들어내는 z를 sampling하는 분포를 추론하기 위해,

x를 evidence로 줬을 때 z를 뽑아낼 수 있는 분포인 $p(z \mid x)$를 구하고 싶지만, 이 분포는 모르기 때문에 $p(z \mid x)$에 대한 근사값을 VI를 통해 구한 $q_{\phi}(z \mid x)$를 통해 z를 샘플링하고 이를 $g_{\theta}$에 통과시켜 x를 생성해낸다.

이러한 구조를 살펴보면 공교롭게도 오토인코더의 형태와 동일하게 된다. 인풋과 아웃풋이 x로 동일하기 때문이다.

그러나 수학적으로는 AE와 VAE는 하등 상관이 없다는 것을 알 수 있다.

AE는 인코더 파트의 manifold learning을 위해 디코더 파트가 붙은 반면, VAE는 디코더파트의 generation을 위해 인코더 파트가 붙었다는 점도 눈여겨 볼만 하다.

loss 함수인 ELBO를 뜯어보면 두가지의 파트로 나눠서 볼 수 있다.

하나는 reconstruction error term이고 다른 하나는 regularization term이다.

reconstruction error term는 $q_{\phi}(z \mid x_{i})$에서 z를 도출하여 디코더의 g를 통과했을 때 값이 x로 잘 만들어지는지에 대한 log likelihood이다. 따라서 $q_{\phi}(z \mid x_{i})$에서의 샘플링을 제외하면 오토인코더의 reconstruction error와 같다.

regularization term은 같은 reconstruction error를 가질 때 기왕이면 $q_{\phi}(z \mid x_{i})$가 prior와 비슷할수록 좋다는 뜻이다. prior는 통제성을 위해 쉬운 분포를 채택하므로 이와 유사할수록 $q_{\phi}(z \mid x_{i})$도 다루기 쉬워질 것이기 때문이다.