Hidden Markov Model, modeling sequence data

해당 포스트는 hmm 강의의 요약입니다. 자세한 내용은 강의를 확인해주세요.

HMM은 sequence data의 분포를 학습해 확률적으로 모델링하는 생성모델입니다.

이 모델이 해결할 수 있는 문제들이 무엇인지를 살펴보며 흥미를 돋워 보겠습니다.

• 특정인의 행동에 따른 날씨 추측
• 떡볶이 소비량에 따른 날씨 추측
• DNA 염기서열에서 어느부분이 유전자인지 추측
• 주어진 단어의 품사 추측

딱 보니까 두개의 sequence 데이터를 이렇게 저렇게 해서 원하는 추측을 해내는 모델인 것을 알 수 있습니다. 그렇다면 HMM이 무엇인지 자세히 알아볼까요?

먼저 Markov model에 대해 자세히 알아봅시다.

1. Markov model

markov model은 markov가정하에 state로 이루어진 sequence를 state transition probability matrix(상태전이확률행렬)로 표현한 것입니다. markov 가정은 시간 t에서의 관측은 가장 최근 r개의 관측에만 의존한다는 가정으로 한 상태에서 다른 상태로의 전이는 이전 상태의 긴 이력이 필요하지 않다는 가정입니다. 이를 수식으로 나타내면 r=1일 때, $P(S_t|S_{t-1},S_{t-2},S_{t-3},…)=P(S_t|S_{t-1})$과 같습니다.

이제 r=1인 markov model의 예를 들어보겠습니다. state = {해, 비} s = [비, 해, 해, 해, 비, 비, 해] 위 예시에서 state는 두가지로 해, 비가 있으며, 이러한 state로 이루어진 sequnce s가 있습니다. 이때 상태전이확률행렬을 만들어봅시다. 총 6번의 transition 중 비에서 해로 넘어가는 것은 2번, 비에서 비는 1번, 해에서 해는 2번, 해에서 비는 1번이므로, state transition probability matrix는

입니다. (이때 1행1열 비->비, 1행2열 비->해, 2행1열 해->비, 2행2열 해->해을 의미합니다.)

이제 Markov model에 대해 알았으니 Hidden markov model에 대해 알아봅시다.

2. Hidden Markov Model (HMM)

Hidden state sequence : $[S_1, S_2, S_3, …, S_{t-1}, S_t]$

Observable state sequence: $[O_1, O_2, O_3, …,, O_{t-1}, O_t]$

HMM은 위와 같이 같은 시간에 발생한 두 개의 state sequence 각각의 특성과 그들의 관계를 이용한 모델링입니다. 이때 hidden state가 Markov assumption을 따르고 observable sequence는 Hidden state에 종속됩니다.

HMM 모델을 시각화하면 다음과 같습니다.

Hidden state sequence는 s1,s2,s3라는 3개의 state를 가지고 각 state마다 o1,o2,o3 중 몇개의 사건들이 관찰됩니다.

같은 그림에 대해 확률을 표시하면 다음과 같습니다.

이때 $a_{ij}$는 hidden state가 i에서 j로 전이될 확률이고, $b_{ij}$는 hidden state가 j일 때 observable state이 i가 관측될 확률입니다.

이를 행렬로 나타내면 다음과 같이 A, B를 얻고, A는 State transition probability matrix라고 하고 B는 emition probability matrix라고 합니다. 이러한 A,B는 HMM 모델에서 학습의 대상이 되는 parameter입니다.

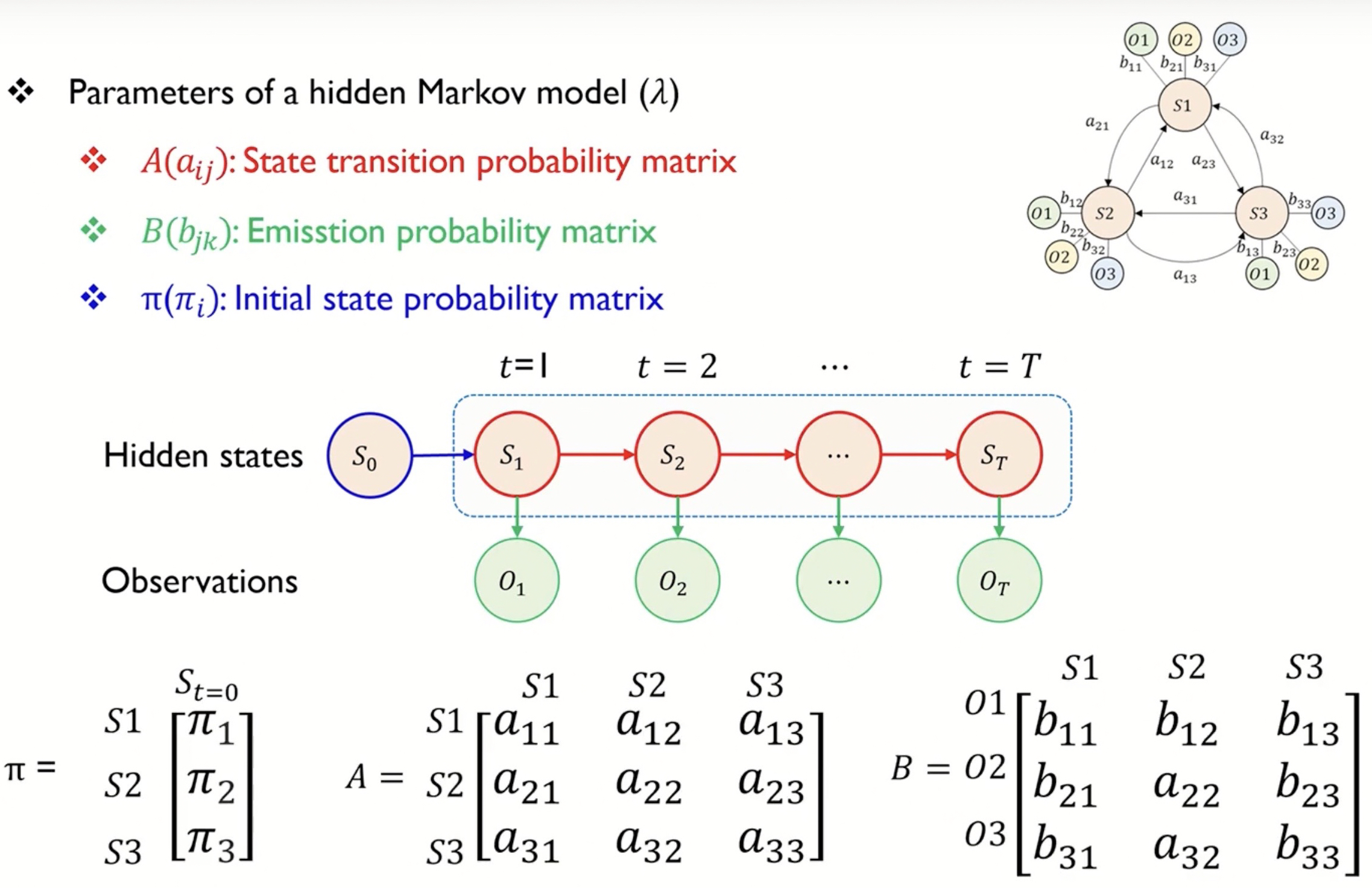
A, B 이외에도 $pi$라는 parameter가 있습니다. 그림에서 $s_1$ ~ $s_t$는 모두 이전의 상태와 현재의 상태 즉 두 개의 상태가 주어질 때 정의되는 상태입니다.